Projection

26243AJ

Directly rendering a voxel world with projected voxels is a powerful technique that allows for realtime* minecraft-like games. By constricting the world to a grid, we can take advantage of many properties of ordered voxels in order to create exceedingly fast rendering engines, vastly surpassing the maximum triangle count for many other polygon-based 3d engines.

Using rotation matrices to optimize projection

The rotation matrix is the cornerstone of projection-based 3d engines. However, polygon-based 3d engines are only able to make use of some of the potential of this matrix.

Although it is natural to think about a rotation matrix as one whole operation which converts worldspace coordinates to cameraspace, when applying the matrix to a grid, it is easier to treat said matrix as a set of individual vectors.

What is a coordinate?
In an unrotated 2 dimensional space, coordinates represent a scale factor applied to 2 vectors. The x coordinate would represent the scale factor of the vector (1, 0), the y coordinate would similarly represent the scale factor of the vector (0, 1), and combining these scaled vectors would result in the final point in space. For simplicity, these vectors will be represented as V.x and V.y respectively. Thus, a coordinate value of (x, y) would be converted into a position in space, represented by P, through the equation P = x*V.x + y*V.y.

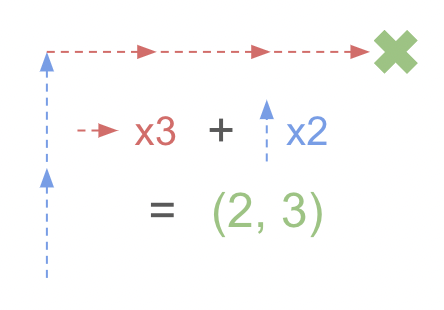
The rotation matrix modifies these initial vectors, replacing them with their rotated counterparts. This, in turn, rotates the point.

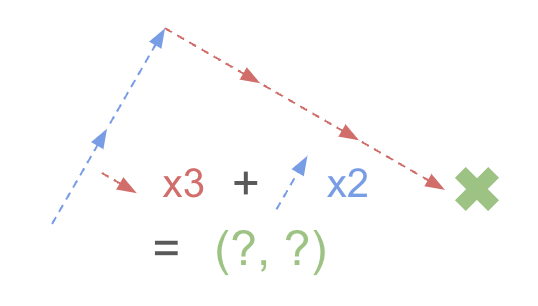
Things become interesting when we move the original point across the two axes, creating a grid.

For example, let’s rotate a line parallel to the x axis formed by a list of coordinates (x, y), (x + 1, y), (x + 2, y), and so on. Applying the operation from above, this would result in a set of points (x*V.x + y*V.y), ([x+1]*V.x + y*V.y), ([x+2]*V.x + y*V.y), and so on. Interestingly, once the initial point has been calculated, the rest of the points can be calculated by simply adding a single vector. If we define our initial point as O = (x*V.x + y*V.y), the next point could be simplified down to O + V.x, and this can be repeated for the rest of the points. By doing so, we are able to reduce an entire matrix multiplication operation for each point down to just a few additions.

This can easily be applied to 3d grids by using a set of 3 3d vectors which represent each axis.

Calculating these vectors is also fairly trivial, as these can be directly obtained from the rotation matrix. By expanding out the matrix into an equation for each axis, we can determine that each column of the rotation matrix equates to the 3 3d vectors we mentioned before.

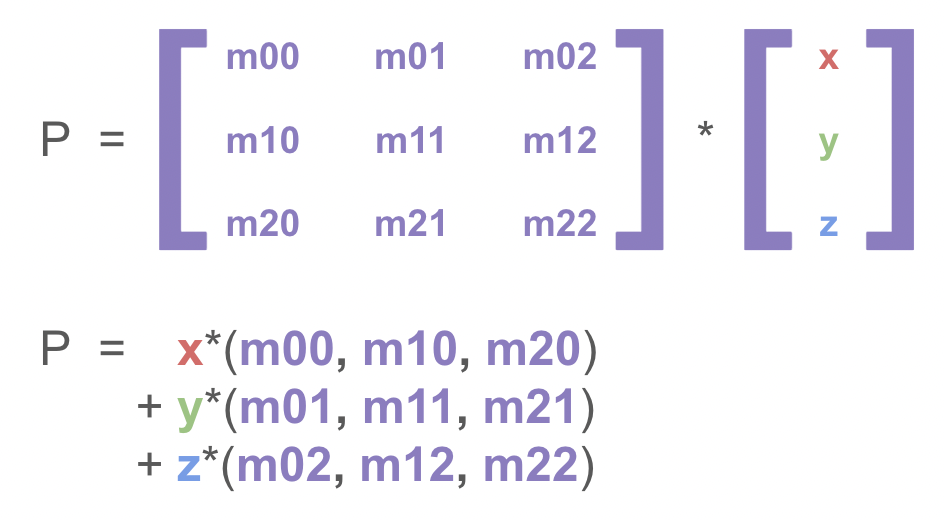
The code implementation of this is shown below, assuming that the rotation matrix has been constructed beforehand and is used like so:
(refer to Rotation Matrix for the construction of this matrix)

Each axis is defined recursively, which simplifies the code

A projection onto the 2d screen is also required, which can be calculated by multiplying the rotated x and y coordinates by FOV/z.
Here is an example of how to render these points:

By combining this with some camera movement code, you will be able to explore a grid of points. You may also want to add z culling, as points behind the camera can appear massive and obstruct your view.

Octant Sorting

26243AJ

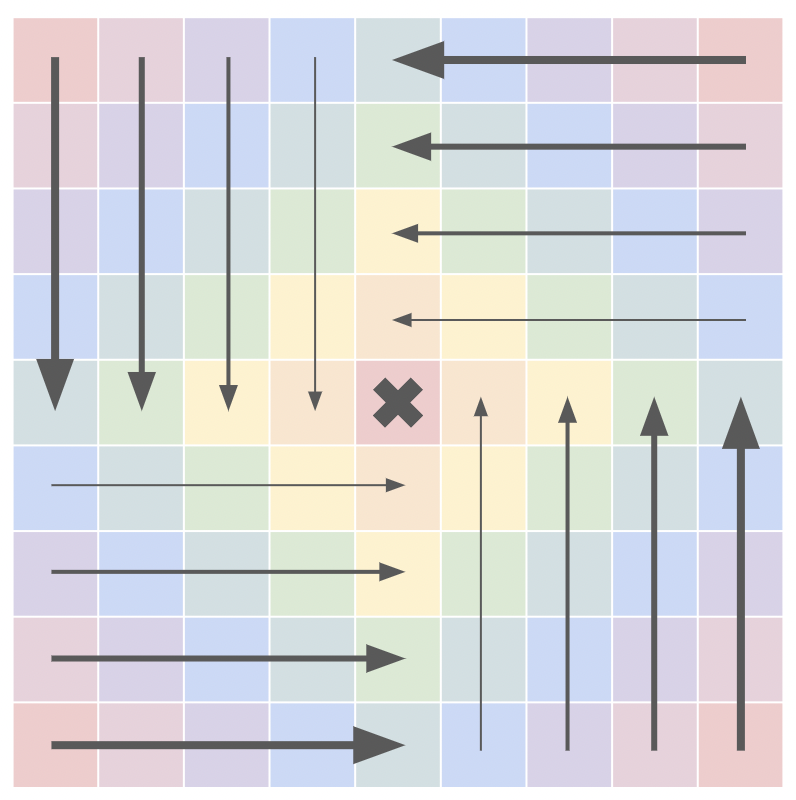
Although rendering the points is fairly simple, efficiently sorting them is another challenge.

It is possible to just input the points into a regular sorting algorithm, and then render them accordingly, however this scales very poorly with the number of points needed to sort for grids (the final render in the previous section contains 8,000 points, and it’s only a 20x20x20 grid).

Octant sorting and its variants overcome this scalability by simply traversing the grid in a certain order, so that all points are correctly sorted. This makes this sorting algorithm an O(n) algorithm, making scale significantly better than other sorting algorithms which commonly range from O(nlog(n)) to O(n^2).

How sorting is done

Similar to many other methods used for 3d graphics, things become simpler and much more manageable when converted to 2d.
By drawing out a heatmap for a 2d grid, we can formulate the order the cells would need to be drawn in order for there to be no sorting errors.

For there to be no sorting errors, the outermost red cells must be drawn first, and then the pink, purple, blue, and so on. This is possible, however there are much simpler options which result in almost identical results.

Instead of traversing the grid in a ring-like pattern, we can instead split the grid into 4 quadrants, and then traverse each of them from back to front. Doing so results in perfect sorting whilst still keeping the algorithm relatively simple.