BVH

BVH, or bounding volume hierarchy, is an acceleration structure that can speed up many algorithms such as collisions, raytracing, BSP tree construction etc. It uses a bounding volume, such as an AABB or a sphere, to contain objects, and then contains the volumes containing objects, hence the hierarchy. The leaf nodes represent the meshes, but can contain more than one object, this is done because usually it isn’t fastest to go that deep into the tree.

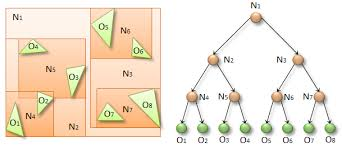
A BVH tree can be any type of tree, but we will be implementing a binary tree here. There are 2 ways to construct a BVH tree, bottom-up and top-down. Bottom-up method makes an AABB around every object in the scene, then connects 2 boxes that are close together, and makes boxes around that, this is repeatedly done until there is only one AABB left which covers the whole scene. Top-down makes an AABB around the entire scene, then chooses a splitting plane to split the scene into 2 regions, it then takes the maximum bounding box in those 2 regions, and repeats the process until every object has its own bounding box.

Construction

For bottom-up, we need to first make a “constructor” list that will be used to construct the tree, for this we need to loop over every object in the scene and find its minimum bounding box, we will be defining AABBs using their minimum and maximum vertex. The minimum bounding box of a sphere can be defined by adding the radius to each component of its position vector for the maximum vertex and subtracting the radius for the minimum vertex and then adding these AABBs to the constructor list, also adding it to a list representing the tree . We then combine the closest boxes together and add those to a different list.

Traversal

Traversal is the same in both methods, make a traversal custom block that has an input for the current node index, when starting traversal just set the index to the index of the root node, then test if the ray intersects with the root node, if it does, recurse down the left and right child nodes by calling the function again, but setting the node index to the index of the left/right child. You can make this faster by prioritizing the closer node first, this is because if the closer AABB happens to be hit, then you won’t have to traverse down the other AABB node, which can save a lot of time. Once the leaf node has been reached, do the intersection tests and simply don’t call the traversal function.