The Basics
World
derpygamer2142, scratchtomv, BamBozzle
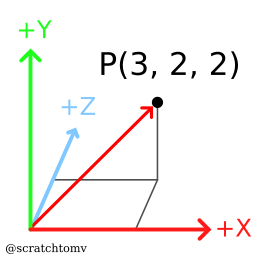
- A standard 3D coordinate system is (x, y, z).
- The coordinate system used throughout this guide looks as follows:
- The
originis the point in 3d space that has the coordinates (0,0,0).
Vectors
derpygamer2142, scratchtomv, BamBozzle
- A vector is a set of numbers similar to a coordinate. They usually describe a movement (called a translation) or direction in space. In 3D, vectors are most often found with 3 values, denoted as x, y and z.
- A vector has a length, or “magnitude”, that can be calculated thusly in 3D: √(x²+y²+z²)
-
A vector with a length of 1 is called a “unit vector”.
-
Dividing each component (x, y, and z) of a vector by the vector's length is called “normalizing”, and results in a unit vector pointing in the same direction.
Geometry
derpygamer2142, scratchtomv, BamBozzle, 26243AJ
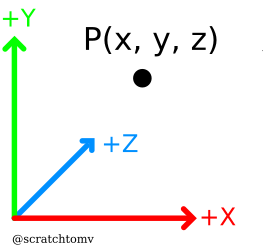
- A point is similar to a vector, having a specific number of values, usually 2 or 3 when working in 3 dimensions. They are used to describe a position in space.
- A ray is a line in space which begins at an origin (a point), and extends infinitely in a particular direction (a vector).

- A plane is an infinite flat surface that extends across space. They can be defined in a number of ways, but most often by their normal (the direction the face of the plane is pointing) and their distance from the origin.
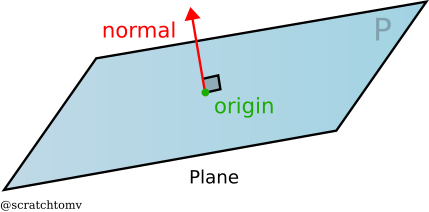
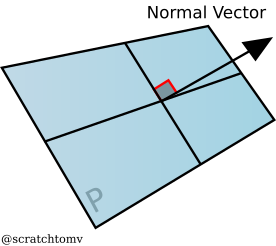
- A normal is a vector perpendicular to a surface. These are often normalized.
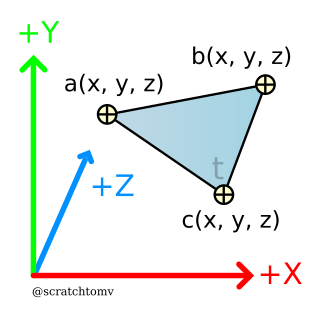
- A triangle is made up of 3 points, with the space between them filled in. Triangles are commonly used in 3d graphics because you can make any shape out of them.
- A quadrilateral (commonly referred to as a quad) is made up of 4 points. Although not many scratch 3d engines directly support the rendering of quads (further elaborated upon in later chapters), they are often used in 3d models, making them an important aspect to consider when creating a 3d mesh / object loader.
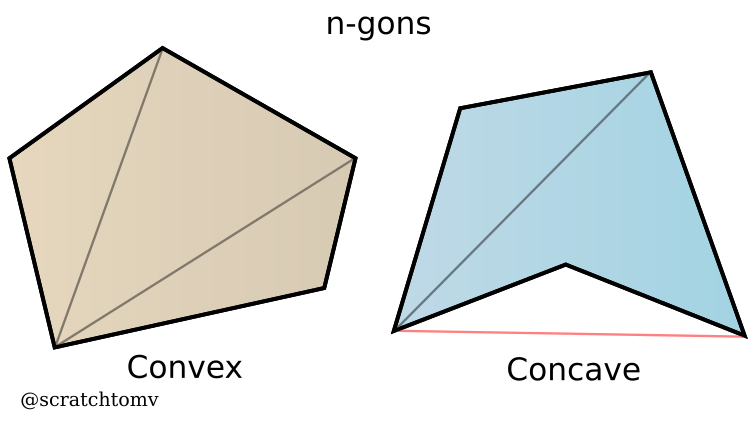
- An n-gon is a shape made up of an n number of points. In scratch these are almost never directly rendered, and are instead split up into many triangles within the object loader. (further elaborated upon in later chapters)
Trigonometry
scratchtomv, derpygamer2142
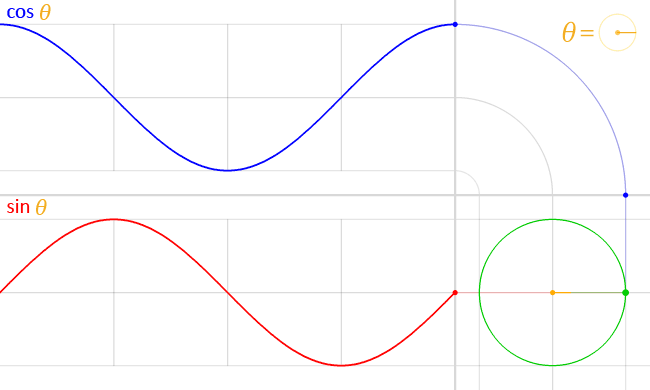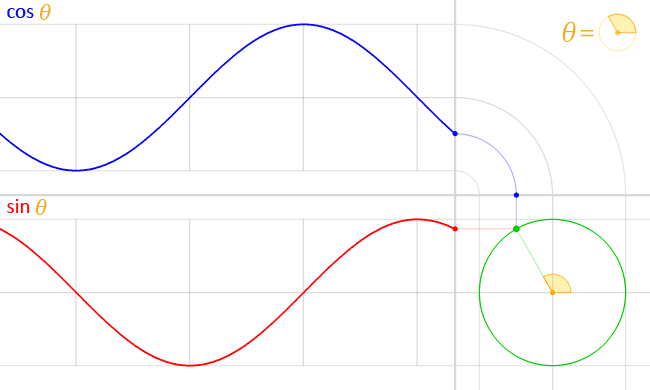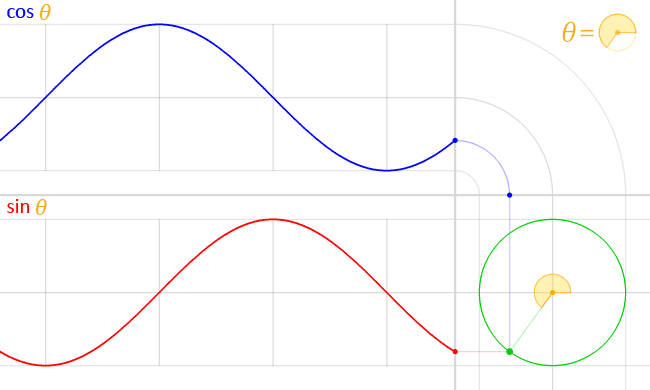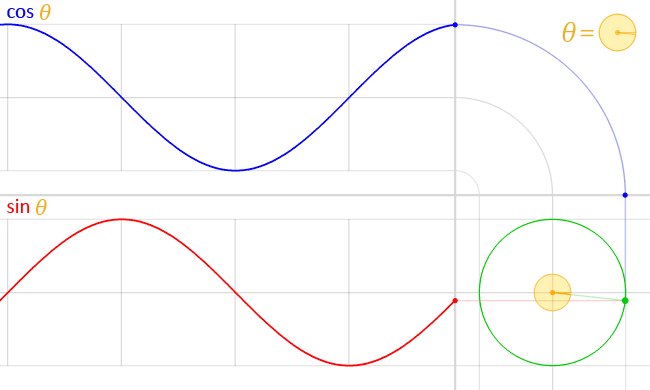
- Sine, cosine, and tangent(often shortened to sin, cos, and tan) and their functional inverses of arcsine, arccosine, and arctangent(asin, acos, atan) are trigonometric functions. They are used to describe the relationship between lengths, angles, and more. The specifics aren’t really relevant to 3d graphics very often, and are mostly used for rotation.
- Trigonometry functions can either use an input in degrees or radians. Radians are a form of describing rotation as a position on a circle with a radius of 1. One full rotation in radians is 2π.
Degrees work the same as radians, but they don’t need π to represent 1 full rotation, hence keeping the calculations simple. One full rotation in degrees is 360 degrees. - You can convert from radians to degrees by multiplying the radians by 180/π, and from degrees to radians by multiplying by π/180. Scratch uses the degrees system, and that is what we will use throughout this guide.
Matrices
badatcode123, derpygamer2142, scratchtomv, Krypto
A matrix is an array of numbers or expressions with rows and columns. Matrices are useful for many things, they make expressing rotations or transformations very easy.
Computations with them will be often simplified in Scratch as literal expressions, so you don’t need to really understand them to make 3D projects.
Matrices can be classified based on how many rows and columns they have, the matrix above is a 2x3 matrix because it contains 2 rows and 3 columns. We can multiply matrices with vectors. However, this isn’t commutative, so you need to be careful about in which order you do this.
An important matrix that is used throughout 3D graphics is the transformation matrix, it is a 4x4 matrix and can be used to convert between world space and a local space, it is often used to convert to camera space. To do this, multiply a vector (the vector being a vertex you are transforming in this case) with the transformation matrix.
In scratch, we usually use 3x3 matrices instead of a 4x4 matrix. We use a 3x3 matrix because it’s much easier to calculate its values, although a 4x4 matrix might make it faster and easier to scale and translate objects.
Matrix multiplication is performed by multiplying the corresponding rows and columns, then adding them together.
Here is an example in which the matrices and
are multiplied.
Rotation Matrix
26243AJ
A rotation matrix is a transformation matrix that is used to apply rotation on a column vector using the right-hand rule. However, due to the nature of matrix multiplication, the right hand rule is only valid when multiplying the matrix by the point and not vice versa.
The 2 dimensional form of this matrix has the following form:
Where θ is the degree you want to rotate the vector by. Using this, a point can be rotated around (0,0) by simply applying matrix multiplication.
Which can be simplified down to
Unlike in 2 dimensions, in the third dimension there are 3 basic rotations: rotation around the x axis, rotation around the y axis, and rotation around the z axis. Thus, there are 3 general rotation matrices for each individual rotation.
These can each be derived from the 2d rotation matrix, by rotating two out of the 3 axes.
For example, the rotation matrix for rotation around the x axis can be derived by keeping the x axis unchanged, and applying the 2d rotation matrix to the y and z axes.
These matrices are listed below:
These matrices can also be combined into one single rotation matrix which applies all 3 rotations at once.