Optimizing critical algorithms
Krypto
RTC Table :
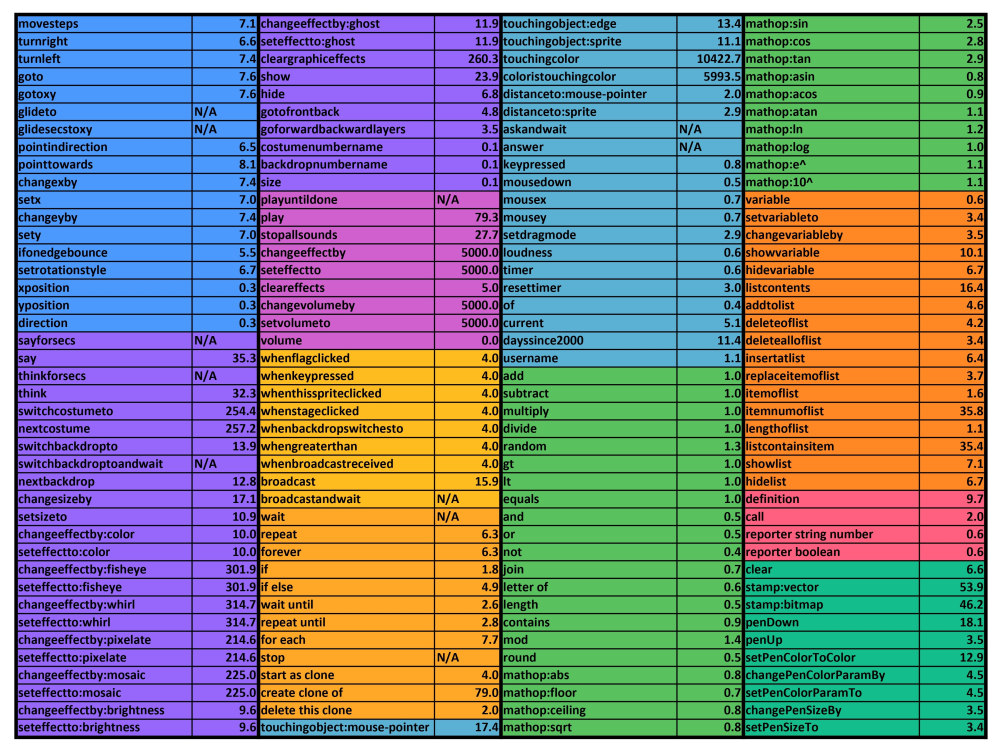 (RTC table by Chrome_Cat on Scratch)
(RTC table by Chrome_Cat on Scratch)
Some of Scratch’s blocks are very slow and should be avoided the majority of the time.
The main blocks you should avoid are the list contains, item # of list blocks (both have a time complexity of O(n)) and touching blocks (Scratch needs to scan the entire stage). As you can see in the chart above, they have an rtc of above 35. Compared to addition blocks, they are at least 35 times slower. In most cases, in 3D you will usually not need to use these blocks.
If you do need to use these blocks (Searching for a name in a list, color scanners etc.) you can probably replace them with better alternatives or bake them at start.
Examples of blocks to avoid :
<touching color () ?>
(item # of [thing] in [Example List v])
<[Example List v] contains [thing] ?>
Complexity
26243AJ
Complexity is a measure of the performance of code when scaled up, and includes both memory and computational efficiency. It is most commonly expressed in Big O notation, which is a mathematical notation that expresses how an algorithm will scale based on the size of the input(s), n.
- For example, an algorithm that gets the first value in a list would be O(1), as even if the list had 20,000 values it would take the same amount of time to compute as a list with 1 value.
- An algorithm that would add up every value in a list would be O(n), since if the list had 100,000 values it would have to add up 100,000 values, and if the list had 2 values it would only have to add up 2 values.
| Most common forms of Big O notation n is the input, c is a positive constant | ||
|---|---|---|
| Notation | Name | Examples |
| O(1) | Constant | Finding the first value in a list |
| O(log(n)) | Logarithmic | Traversing a tree / a binary search |
| O(n) | Square root | Adding up all color values in the first column of a square image |
| O(n) | Linear | Adding up all values in a list |
| O(nlog(n)) | Loglinear, Linearithmic | Common sorting algorithms, such as quicksort and merge sort |
| O(n^2) | Quadratic | Naive collision algorithms, insertion sort |
| O(n^c) when c > 1 | Polynomial, Algebraic | [EXAMPLES NEEDED] |
| O(c^n) when c > 1 | Exponential | [EXAMPLES NEEDED] |
| O(n!) | Factorial | bogosort |
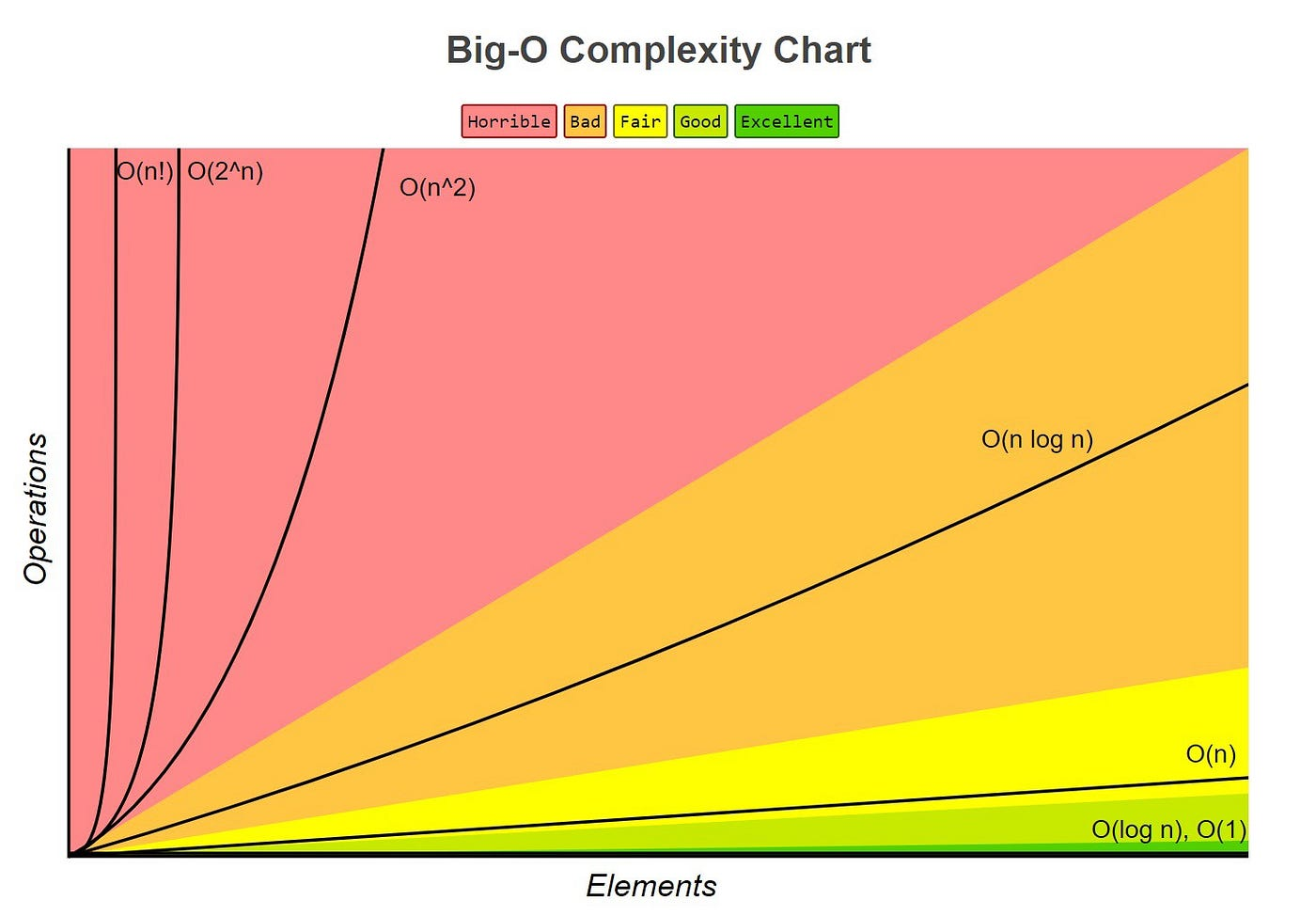
Important things to consider with Big O notation:
- Ignore Constant Multiplication; if a linear algorithm is twice as slow as another linear algorithm, it may be tempting to write it as O(2n). However, the big O represents all scaling factors, thus the 2 would be factored out and the expression would be written as O(n)
- Ignore less-significant terms; if an algorithm contains both O(n) and O(n^2) components, it may be tempting to write it as O(n^2 + n). However, big O notation only focuses on the fastest growing factors, which in this case would be n^2. Therefore, it would be written as O(n^2)
- A less-significant big O does not signify that an algorithm is better; Big O only shows a snapshot of how an algorithm scales, not how well it will perform in practice. At first glance, an algorithm that scales in O(log(n)) may seem better than an algorithm that scales in O(n), however, on small scale data sets the O(n) algorithm may perform better if it has a smaller O than the O(log(n)) algorithm. Although Big O notation can be very useful in providing a quick summary on how well an algorithm will perform, it should only be used as a rough guideline and it is still important to test the speeds of algorithms yourself.